- For Science
- The Smaller the Merrier
- Ambitious or Crazy?
- Anatomy of an LLM
- Parallel Computing is Tricky
- SIMD is the Necessary Evil
- What's Next?
For Science
It all started on a rainy afternoon in Vancouver when the research team set a meeting with engineering to pitch picoLLM Compression, a novel Large Language Model (LLM) quantization algorithm. The request was to build an inference engine for picoLLM compressed models, which later became the picoLLM Inference Engine. The SDEs' initial excitement 🤩 quickly turned into eye-rolling 🙄, fear 😟, and panic 😱!
picoLLM Compression is an LLM quantization algorithm that learns the optimal bit allocation strategy across and within weights. A picoLLM-compressed weight contains 1, 2, 3, 4, 5, 6, 7, and 8-bit quantized parameters. Hence, a weight doesn't have a bit depth and instead has a bit rate. For example, if the bit rate of weight is 2.56, every floating-point parameter in the matrix is compressed to 2.56 bits on average.
Even though extremely powerful, picoLLM Compression poses a complex inference challenge. Existing quantized LLM inference frameworks assume a constant bit depth within a weight. Also, the majority focus exclusively on 8-bit and 4-bit quantization. Hence, we had to create an inference engine to handle X-Bit Quantized LLM inference.
The Smaller the Merrier
Compressing LLMs eases their storage and reduces the required RAM for inference. These are the concrete advantages of compact LLMs, even when we go below the dreaded 4-bit precision. However, two common concerns hinder the adoption of deeply-quantized (sub-4-bit) LLMs:
- Accuracy loss.
- Speed drop: 8-bit and 4-bit quantizations are inference-friendly, while 1, 2, 3, 5, 6, and 7-bit operations are inherently slow as they require more instructions.
picoLLM Compression effectively addresses the first issue.
The second concern is only historically valid when the model sizes were in millions of parameters, as the compute resources were the bottleneck. However, memory access becomes a blocker when the model sizes grow to billions of parameters. Below, we show an empirical benchmark in support of the above argument. We compress Llama-2-7b using picoLLM Compression at different sizes and measure their speed, i.e., tokens per second. The benchmark ran on an AMD Ryzen 7 5700X 8-Core Processor. As we make the model smaller, it runs faster.
Ambitious or Crazy?
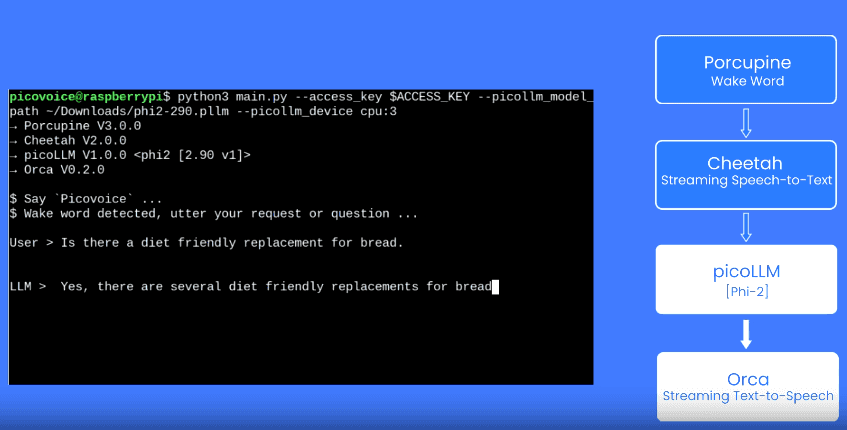
OK. We were motivated but needed to figure out if we could deliver. Initially, the task sounded crazy. Why? The request was to create an inference engine across Linux, macOS, Windows, Android, iOS, Raspberry Pi, Chrome, Safari, Edge, and Firefox. They also wanted it to support CPU and GPU and have the architecture to support other forms of accelerated computing (e.g., NPU). Last but not least, it had to be able to run any LLM architecture. 🤯 💩
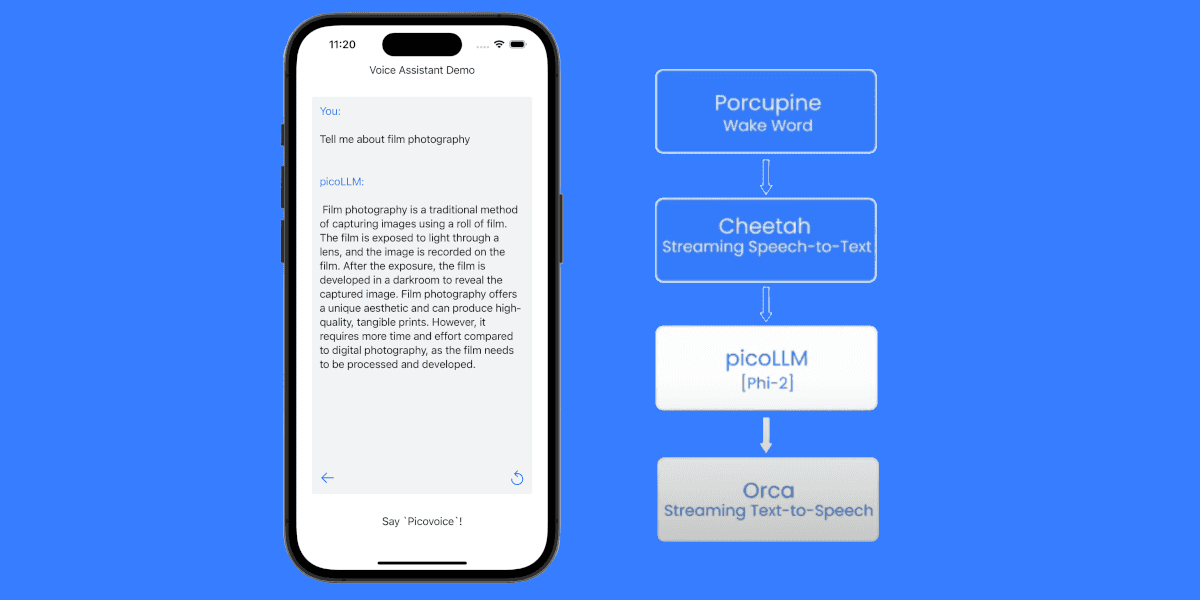
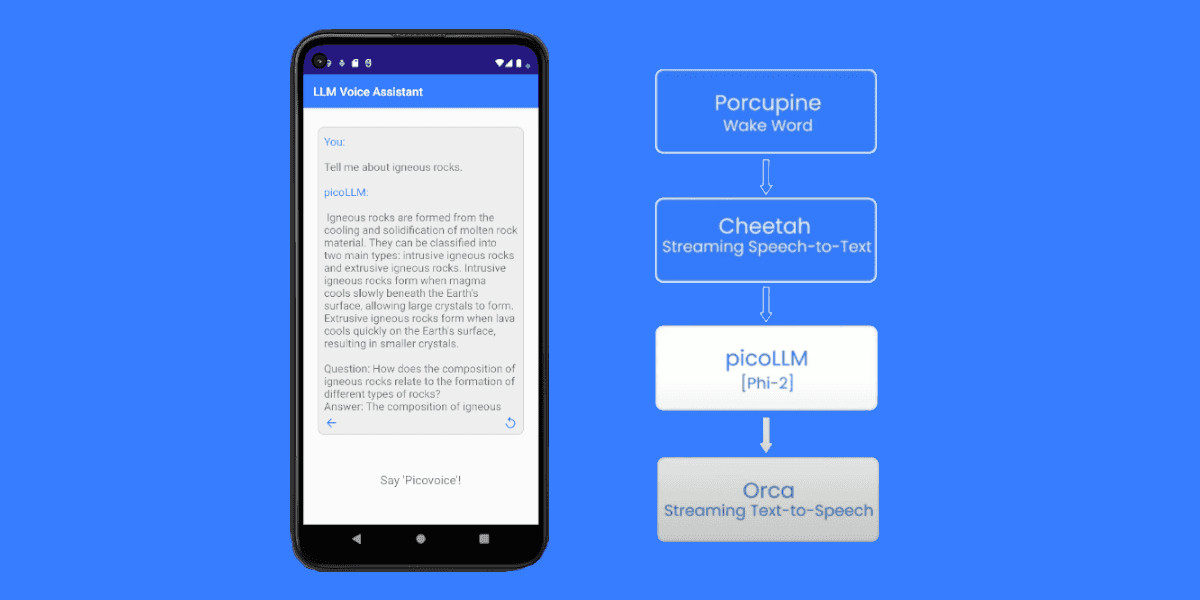
But we have done crazy before, like when we were asked to run a complete Voice Assistant locally on Arduino! [🎥]
We (somehow) made it, which is why we are still employed to write this therapeutic 💆 article. Below, we document how we climbed this hill and what we learned.
Are you a deep learning researcher? Learn how picoLLM Compression deeply quantizes LLMs while minimizing loss by optimally allocating bits across and within weights [🧑💻].
Are you a product leader? Learn how picoLLM can empower you to create on-device GenAI features [🧑💻].
Anatomy of an LLM
First, we had to learn enough about the internals of LLMs to implement an inference engine for them. Before delving into the details, let's familiarize ourselves with the terminology. We've all come across terms like GenAI, LLM, and Transformer. An LLM is an application of the Transformer architecture. GenAI is the term commonly used in business circles for LLMs. In summary:
- Transformer ➔ 🧠
- LLM ➔ 👷
- GenAI ➔ 👨💼
In our experience, as SDEs, it is best to ignore the whys of math and simplify the problem to a graph traversal where each node represents a well-defined computational operation. Our job is to traverse the graph and perform the computations as quickly as possible.
Below is just an elementary introduction to what we learned.
LLM
We all have used ChatGPT or one of its friends. So, we use that as a starting point to explain how an LLM works. An LLM accepts a piece of text known as a Prompt as input. That is the question you pass to ChatGPT. The output of LLM is also text, which is known as Completion. This is the answer you get from ChatGPT. Let's see what happens inside.
First, the text is transformed into a sequence of integers because neural networks can work with numbers, not text! A module called Tokenizer transforms text into integers:
Once we have the tokens, we convert them into a sequence of floating-point vectors called Embedding. The conversion from tokens to embeddings is essentially a lookup table (LUT) operation, where each token index corresponds to an embedding vector.
Once we have the embedding, we pass through a chain of Transformers—more on the transformer below. A transformer accepts a sequence of floating-point vectors and returns one with the same shape. The number of transformers in open-weight LLMs is in 10s.
We grab the output of the last transformer and pass it through Softmax, which gives us another floating-point vector representing the probability of the next token.
We pass this on to a module called Sampler, which picks the next token. There are many sampling strategies. The need for samplers is twofold: First, to give slightly different answers to the same question so the chatbot feels like a person, and second, to prune dumb (unlikely) answers.
Finally, we decode this token and create bytes representing the next piece of text (answer). This is again fed into the LLM to process the next piece, and so on.
Transformer
There are two main components in a Transformer: Attention and FeedForward. Unfortunately, no standard form for a Transformer exists, and DL researchers have developed many variants. The pictures below show the architecture of the Transformer modules used in Llama-2 and Phi-2.
One of our requirements was to run any LLM architecture, which means we must accommodate all these variables without hard-coding them in C. The solution again was to think of a transformer as a computational graph and each node as a compute module. Then, all that needs to happen is serializing the graph and finding a way to traverse it.
Attention Mechanism
The attention mechanism is more or less constant across the LLMs 😌.
FeedForward
Again, the feed-forward module is not standard and varies significantly across LLMs. We used the same graph serialization technique to handle many forms of FeedForward networks. The pictures below show the architecture of the feed-forward modules used in Llama-2 and Phi-2.
Parallel Computing is Tricky
Look at the graphs above describing various parts of transformers. You can see that there are often parallel paths that we can traverse concurrently. CPUs and GPUs can run things in parallel, and we should take advantage of this to speed up the inference. Hence, we need to run the graph in parallel. The figure below shows the concept for the attention module. If we run the graph sequentially, there are nine steps, but we can run in 5 steps if we use parallel computing.
CUDA has a built-in mechanism for parallelism, as do other accelerated computing frameworks, such as Apple Metal and WebGPU. On CPUs, we use threads directly. Except for the Web! Because there is no threading support in JavaScript 🤦♂️ ... We had to build our threading framework for the web using WebWorkers.
SIMD is the Necessary Evil
Parallel computing is one way of gaining speed. The other orthogonal method uses multiple computations (e.g., additions) using a single instruction. This is called Single Instruction Multiple Data (SIMD). x86-based CPUs have SSE, AVX, AVX2, AVX512, ... Arm Cortex-A based CPUs have NEON, SVE, ... Figure below shows gains achieved by using SIMD on an x86_64 Intel CPU when running Llama-2-7b.
In an ideal world, the compiler should automatically take advantage of these. It does if you do your operations in a reasonable bit depth (e.g., 32, 16, or 8), but once you try to do 7-bit multiplication, you are on your own. The compiler in our experiments did nothing automatically. The math we are implementing here is very upside down.
While SIMD may initially seem straightforward, it requires more than just sprinkling magic functions on your C code. We encountered two major challenges.
Consider this scenario: we are shipping a Linux library that needs to support all architectures (SSE, AVX, etc.), but we have no knowledge of the target computer's capabilities. We had to develop a system that can detect capability at runtime and select the most suitable code.
There is just too much code to write. Let us explain why. Let's consider the weight multiplication function. The below is a reasonably accurate signature for it. A matrix is some packed data with 1, 2, 3, ..., or 8-bit parameters. X is the input, and y is the output.
First, we must develop eight different variants for each bit-depth. These are inline helper functions, and the primary function above makes calls depending on the region of the weight.
There are situations where the input to the function is more efficient when quantized to 8 bits. Hence, we must develop two versions for each bit depth above. this is 16 implementations.
Now, for each of the 16 implementations, we need an implementation for each SIMD available. For x86, there are many variants, but we restricted ourselves to 5. Hence, we have 80 functions to write for ding matrix multiplication on x86.
Arm CPUs and CUDA share the same story. Also, keep in mind that many other functions need to go through this process.
What's Next?
Start Building
Picovoice is founded and operated by engineers. We love developers who are not afraid to get their hands dirty and are itching to build. picoLLM is 💯 free for open-weight models. We promise never to make you talk to a salesperson or ask for a credit card. We currently support the Gemma 👧, Llama 🦙, Mistral ⛵, Mixtral 🍸, and Phi φ families of LLMs, and support for many more is underway.
o = picollm.create(access_key,model_path)res = o.generate(prompt)